Estimation of Cini for Modelling Observed Events
Data requirements
To model observed events, it is necessary to collect and store different sets of hydrometric data, both at a sub daily (hourly or 15 minutes) and daily intervals. The data requirements for each individual event are summarised on Table 9.
Table 9. Hydrometric data requirement for estimating ReFH model parameters from each observed flood event
| Data type | Time step | Description |
|---|---|---|
| Rainfall | Average \Deltat | Catchment average event rainfall of timestep Δt forming the event hyetograph. Imported to ReFH2. |
| Rainfall | Daily | Catchment average rainfall for the period leading up to the day of the start of the selected event, enabling estimation of initial soil moisture content, C_{ini}. Imported to ReFH2. |
| Evaporation | Daily | Potential evaporation for the period leading up to the day of the start of the selected event, enabling estimation initial soil moisture content, C_{ini}. Estimated by ReFH2 from an average annual potential evaporation. |
Rainfall Data
Figure 7 shows the definition of observed rainfall. The data requirements for analysis of the event using the ReFH2 observed event functionality are indicated.
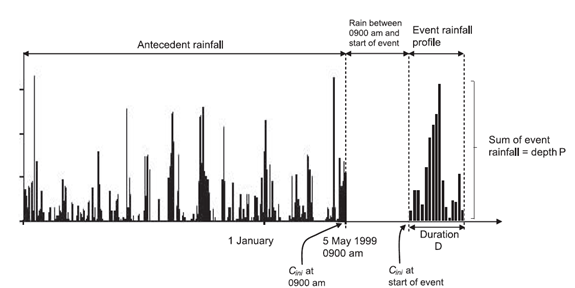
Figure 7. Definition of rainfall event inputs
Note that in the ReFH model it is conventional to store rainfall data against the beginning of the time step under consideration, e.g. the rainfall falling in the hour between 10:00 and 11:00 will be stored at 10:00.
In general, most of the collected hydrometric data must undergo some appraisal and processing before the flood event analysis can proceed. In addition to catchment average sub-daily event rainfall data catchment average daily timeseries antecedent rainfall and potential evaporation are required.
Review of both the event and antecedent data are an integral part of ensuring the modelling exercise is conducted with due hydrological rigor. In the context of the event due consideration to rainfall gradients and accuracy of measurement must be given and it is recommended that a BSI method for rainfall interpolation from gauges to catchment is adopted if raw rain gauge data are to be used.
Catchment daily rainfall data may be derived from source rain gauges and the reader is referenced to the BSI methods for appropriate interpolation procedures. However, the Centre for Ecology and Hydrology Gridded Estimated of Areal Rainfall (GEAR dataset) publishes gridded daily rainfall data at a 1km² resolutions for Great Britain and it is recommended that these data are used, where possible, for estimating catchment daily rainfall series.
Distinguishing between event and antecedent rainfall is best achieved by plotting the rainfall and flow together, whereby it is usually possible to infer the bursts of rainfall that were directly responsible for the event. However, a certain amount of judgement has to be applied, for example in deciding whether to divide a multi-burst storm into antecedent rainfall (contributing to the initial soil moisture content) and event rainfall (contributing directly to the flood event). In practice this is not so critical for the ReFH2 observed rainfall functionality, as the water balance option of the model is used. As discussed under Water balance closure in the Rural model the simulation is subdivided into segments equivalent to the recommended duration with updating of the soil moisture content, C_{(t)} at the end of each segment to reflect the generation of baseflow during the segment. Thus the event model will not develop unrealistically large values of soil moisture content if the event model is applied prior to the actual start of the event.
Potential Evaporation Data
Within ReFH2 the daily antecedent Potential Evaporation is estimated using a simple estimate of the average annual Potential Evaporation (PEann) which is then distributed as a daily evaporation across the year as a sinusoidal form peaking in the summer months:
where n is the day of the year. Potential Evaporation is usually expressed as an evaporation for a reference, short grass crop with unlimited access to water, it is thus a modelled estimate rather than a measurement.
ReFH2 provides graphical methods and summary statistics for optimising the modelling of antecedent soil moisture conditions, the actual source of the reference estimate and the exact form of within year variation is less critical. Potential evaporation estimates are published on a daily timestep for every 1km² cell for Great Britain by the Centre for Ecology and Hydrology as part of their CHESS dataset.
Deriving an estimate of Cini based on antecedent weather conditions
C_{ini} is estimated within ReFH2 through the application of the DAYMOD daily soil moisture accounting procedure. This procedure conceptualises the soil column as retaining a maximum mean moisture depth equal to the Field Capacity (FC) (mm). Evaporation can take place from the soil column thus depleting the soil column mean moisture depth, m(t), over a timestep in the absence of rainfall. Evaporation takes place at the potential rate until a lower threshold is reached, the Rooting Depth (RD), beyond which evaporation takes place at a reduced rate. The magnitude of the reduction is proportional to the difference between the soil moisture depth, m_{(t)} and RD.
If the soil water depth exceeds FC this water is available to fund evaporation, but also a proportion of the depth of water in excess of field capacity will drain. The drainage rate is proportional to the depth of water above FC. If rainfall is incident when m_{(t)} is ≤ FC with a time step then m_{(t)} will increase or decrease depending on whether the rainfall is larger than the evaporation demand, or not. Above FC then m_{(t)} will increase if the rainfall is larger than the sum of evaporation and drainage.
The maximum mean soil moisture depth is SM. ReFH conceptualises the distribution of soil moisture depths across a catchment as a uniform distribution across the range [0,C_{max}]. Thus:
This is a variation of the well-known FAO56 soil moisture accounting procedure and is presented diagrammatically in Figure 8. The drainage from DAYMOD averaged over a year is an estimate of the mean runoff from the catchment over the year. The full mathematical formulation of DAYMOD is presented in Appendix A of the FEH Supplementary Report No1 (Kjeldsen, 2007). This includes the proof that:
Thus C_{ini} is estimated from the value of m_{(t)} at the start of the event.
Parameterisation of DAYMOD
DAYMOD has four parameters:
- FC – field capacity (mm)
- RD – rooting depth (mm)
- SM – maximum mean soil moisture content (mm)
- DK – drainage coefficient
And from trigonometry SM is C_{max}/2. For the ReFH2 observed rainfall application DAYMOD is used to estimate C_{ini} for the start of the observed event. The following default parameter relationships are used:
where SM{'} is a dimensionless scalar. For the calculation of default parameters SM{'} is set to 3.
As discussed, if the soil moisture depth within a timestep m_{(t)}>RD, evaporation takes place at the potential rate; if m_{(t)}<RD the evaporation reduces linearly according the ratio m_{(t)}/RD. If m_{(t)} > FC then drainage can occur according to D(t)= k(m_{(t)}-FC) and a daily drainage rate of DK=e^{-k\Delta t} = 0.8 is set as the final default parameter.
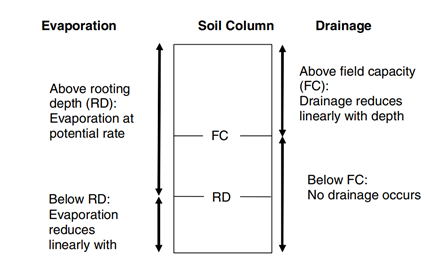
Figure 8 The conceptual structure of the DAYMOD daily soil moisture accounting procedure
As for design events, the simulation of observed events is very sensitive to the estimate of C_{ini}. It is strongly advised that the DAYMOD simulation is examined carefully with appropriate interventions regarding parameter choices. The objective is to ensure that the within year variation of the simulated catchment soil water regime is representative of what might be expected for the climatology and soils of the catchment being modelled. To support this, the observed modelling option within ReFH2 provides summary statistics over the period of simulation of total:
- Actual Evaporation loss (mm)
- Effective Rainfall (runoff) (mm), and
- Precipitation (mm).
Additionally, the software graphs the daily variation in Precipitation, Potential Evaporation together with the mean soil moisture depth (with FC and RD marked for context to aid the interpretation of the variation in soil moisture depth).
The parameters FC, RD and DK can be adjusted to achieve a sensible model of the catchment soil moisture regime. It is recommended that this is achieved by adjusting FC and RD (although DK can be adjusted) subject to the constraint SM>FC>RD. The following general hydrological observations (rules of thumb) are made to aid this interpretation of what is a sensible water regime:
- If the average annual rainfall of a catchment is typically greater than 850mm then evaporation will take place at the potential rate other than for extended periods of dry weather. In dryer catchments evaporation may reduce below the potential rate for significant periods of time during the summer months.
- The difference between FC and RD would be expected to be dependent upon both soils and vegetation. However, for a given vegetation type it is likely to be greater for permeable soils than impermeable soils.
- Over a year, and particularly if the values of soil moisture m_t at the start and end of the period are similar, the average drainage depth should broadly be equivalent to the average runoff observed at nearby gauging stations over the same period.
In application, the suggested minimum period for modelling the antecedent soil moisture is one year. However, it is axiomatic that the more years that are modelled the greater insight into the soil moisture regime and whether the simulations of annual runoff can be reconciled with gauged estimates over the same period.
Gustard et al (1992) published a simple water balance model using long term annual estimates of SAAR4170 and Penman PE. Although there are now more sophisticated generalised models for estimating mean annual runoff used operationally in the UK these methods are based on daily rainfall runoff models that include a conceptual representation of representing soil and vegetation characteristics into account (Holmes et al, 2002). However, Holmes et al (2002) also published an updated form of the simple equation of Gustard et al (1992), re-calibrated for SAAR6190 estimates and, more importantly, Penman Monteith estimates of PE which tend to be higher. The form of this equation is:
Where:
r = 0.00091 \times (SAAR6190 + 0.13) for SAAR6190 < 850mm
r=1.0 for SAAR6190 \geq 850mm
This equation can be used as a simple comparator for evaluation whether the mean runoff from DAYMOD is reasonable. If the rainfall over the antecedent period is significantly different from the SAAR value this can be used, with caution, within this equation. It is recommended that both the application of this equation and evaluation of the corresponding mean runoff over the common period at nearby gauging stations with similar values of SAAR6190 are considered when evaluating whether the drainage estimates, and hence soil moisture regime modelled by DAYMOD is reasonable.