Estimates for Model Parameters in Ungauged Catchments

The previous section described the estimation of the design rainfall hyetograph for a specified frequency for use in the ReFH2 design package.

Within the design package application, the ReFH2 model is used in conjunction with design initial conditions and model parameters that have either been estimated from flood event data or catchment descriptors. These descriptors summarise the physical attributes of the catchment such as area, soil properties, general wetness and degree of urbanisation application. It is recommended that wherever possible flood event data should be used within parameter estimation. Formal calibration of the model parameters from event data should be undertaken where possible and requires good quality flood event flow and rainfall data sets. However, a more rapid calibration of the Tp parameter only can be undertaken using either discharge or level data. This could be based upon the analysis of rainfall lags as discussed within the Environment Agency’s Flood Estimation Guidelines or by sequential modification of the Tp parameter directly within ReFH2 using the observed event modelling function for a number of events.

This section presents the estimation of model parameters from catchment descriptors in the absence of observed event to calibrate the model against - the ungauged catchment case. When ReFH2 is used for design event estimation the model initial conditions are also estimated as part of the design package. This estimation is described in Initial Conditions Design Estimates.

Rural Model Parameters

In the absence of observed data, the model parameters and initial conditions for the as rural model are estimated from catchment descriptors using design equations. These have been developed using multivariate regression analysis to relate the variation in calibrated model parameters between catchments to catchment descriptors describing the topography, soils, climate and drainage network characteristics of the catchments. There are separate sets of parameter equations for Scotland and the group of England, Wales and Northern Ireland.

The development of these equations is presented in ReFH2 Science Report: Model Parameters and Initial Conditions for Ungauged Catchments$^{R1}$. The form of the equations and the sensitivity of the equations to the explanatory catchment descriptors is presented within this section and the model coefficients are presented as contextual information within the in-software help. The general form of the equations for estimating model parameters within the UK is shown in Table 6.

Latest research during the Small Catchments Project Phase 1 Environment Agency (2012) and Phase 2 has shown that FEH methods are more accurate than methods such as IH124 for both estimating peak flows within small catchments and for conducting plot scale greenfield runoff calculations. ReFH2 is a recommended method within the 2015 CIRIA SuDS Manual for undertaking the estimation of greenfield runoff rates and volumes. ReFH2 is also a recommended method for undertaking the estimation of post development runoff rates and volumes for simple developments.

The inclusion of the catchment drainage network geometry descriptors $DPLBAR$ (mean drainage path length) and $DPSBAR$ (mean drainage path slope) in the equations for $Tp$ and $BL$ in the catchment parameter equations limited the usefulness of the model for estimation of flows at the plot scale. The ReFH2 “plot scale” models to estimate these parameter values use $AREA$ as an alternative descriptor to $DPLBAR$ and $SAAR$ as an alternative to $DPSBAR$. Hence, ReFH2 can be used directly to estimate greenfield runoff rates and volumes at the plot scale. See Drainage design applications for further details of using ReFH2 for drainage design.

These “plot scale” equations can also be useful for catchment level estimation within very small catchments or catchments where the catchment topography and hence drainage network geometry descriptors of $DPLBAR$ and $DPSBAR$ lie towards the extremes of what might be expected for a catchment of a given scale. Examples of these include very linear catchments, draining through incised valleys with short tributaries, such as some of the catchments in the valleys of South Wales.

Across small catchments (area less than 40 km$^2$) the estimates generated using the plot scale and catchment scale equations for $Tp$ and $BL$ are broadly similar. Thus, in practice, if large differences are observed in the estimates it is recommended that the user should investigate these differences to decide whether the network descriptors lie towards the margins of what is typical in a UK context. To aid this interpretation the relationship between $DPLBAR$/$AREA$ and $AREA$ and $DPSBAR$/$SAAR$ and $SAAR$ are presented on Figure 6.

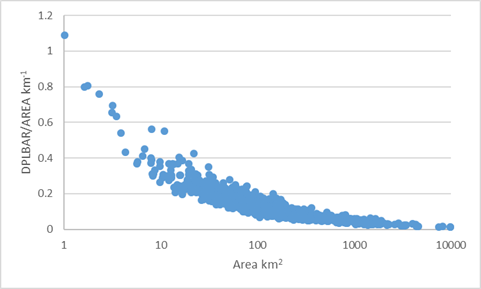
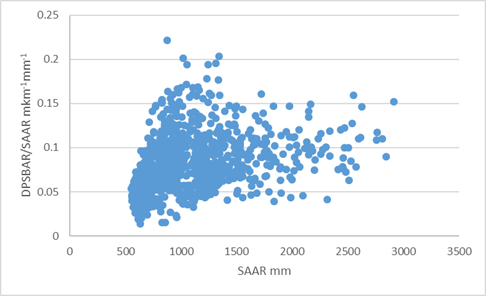
Figure 6. Ratio of DBLBAR and AREA as a function of area and DPSBAR and SAAR as a function of SAAR

Table 6. Structure of equations estimating ReFH2 model parameters

ReFH parameter	Application	Parameter estimation equation
$Tp$	Catchment scale	$Tp = aPROPWET^b\cdot{ DPLBAR^c}\cdot{ DPSBAR^d}$
	Plot scale	$Tp = aPROPWET^b \cdot{AREA^c} \cdot{SAAR^d}$
$C_{max}$	Catchment and plot scale	$C_{max} = aPROPWET^b \cdot{exp(cBFIHOST)}$
$BL$	Catchment scale	$BL = aPROPWET^b \cdot{DPLBAR^c} \cdot{BFIHOST^d}$
	Plot scale	$BL = aPROPWET^b \cdot{AREA^c} \cdot{BFIHOST^d}$
$BR$	Catchment and plot scale	$BR = aPROPWET^b \cdot{BFIHOST^c}$

* Note that URBEXT2000 was included in the derivation of the equation coefficients for $Tp$ and $BL$, but is not used in the estimation of the ‘as rural’ parameters as the influence of urban landuse on the flood hydrograph is incorporated explicitly within the ReFH2 urban model.

$$$$

The predictive performance of the equations for estimating $Tp$, $C_{max}$, $BL$, and $BR$ are summarised in Table 7 and Table 8 for catchment and plot scale applications.

$$$$

Table 7. Fit statistics for ReFH2 parameter equations (England, Wales and Northern Ireland).

ReFH parameter	Application	R²	Standard Error
$Tp$	Catchment	0.80	1.3
	Plot scale	0.71	1.36
$C_{max}$	Catchment and plot Scale	0.6	1.29
$BL$	Catchment	0.35	1.49
	Plot scale	0.31	1.48
$BR$	Catchment and plot Scale	0.36	1.51

$$$$ Table 8. Fit statistics for ReFH2 parameter equations (Scotland).

ReFH parameter	Application	R²	Standard Error
$Tp$	Catchment	0.68	1.37
	Plot scale	0.73	1.4
$C_{max}$	Catchment and plot Scale	0.57	1.15
$BL$	Catchment	0.72	1.2
	Plot scale	0.73	1.2
$BR$	Catchment and plot Scale	0.22	1.4

Urban Model Parameters

The response of the urban model is controlled by five parameters with corresponding parameter estimates:

• Urban area (km²) – the default estimate is based on the $URBEXT_{2000}$ catchment descriptor
• The Impervious Factor ($IF$) – optimisation of the urban model in explaining as-rural model residuals for all
• $IRF$
• $DS$
• $Tp Factor$

The structure and the default parameterisation of the urban model is presented in detail in the Urban Model section. The main point to be emphasised is that although these default values were identified by maximising the average performance of ReFH2 in urbanised catchment, urbanised catchment are difficult to model.

This difficulty arises because, amongst other issues, the hydraulics of the conveyance of drainage systems are complex, as are the relationship between impervious surface and pervious surface runoff and the positive drainage of these surfaces.

The transparency of the ReFH2 representation of the urban area does enable the user to move away from these default values in a considered way. The first three parameters can be revised based upon maps (or survey) and local knowledge of the drainage system catchments. The $Tp Factor$ can be revised though analysis of river flows data if these are available. The Urban Model section discusses the revision of model parameters in more detail.

In extreme cases, where the runoff response of a catchment is primarily a function of the configuration and operation of the urban drainage system, it is suggested that the catchment might be more fruitfully modelling using an urban drainage system approach focusing on the hydraulics and operation of the drainage system.